Marcelo abrió su cuaderno y comenzó a estudiar fracciones para la prueba. Recordó que éstas representan un conjunto de partes de un entero, y repasó cómo se comparan. Pensó entonces que le era más fácil comparar ciertas fracciones calculando cuánto le falta a cada una para completar el entero. Por ejemplo, a  le faltan 5 partes para completar el entero, mientras que a
le faltan 5 partes para completar el entero, mientras que a  le falta solamente 1. Marcelo concluyó entonces que
le falta solamente 1. Marcelo concluyó entonces que 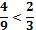 .
.
Un estudio realizado en el CIAE indagó en las estrategias que utilizan escolares como Marcelo, en el segundo ciclo de enseñanza básica. Con alrededor de 500 participantes de diversos colegios de Santiago, el estudio encontró una variedad de modos de pensar sobre las fracciones. Algunos de éstos no son enseñados en la escuela, sino que son ideados por los mismos estudiantes.
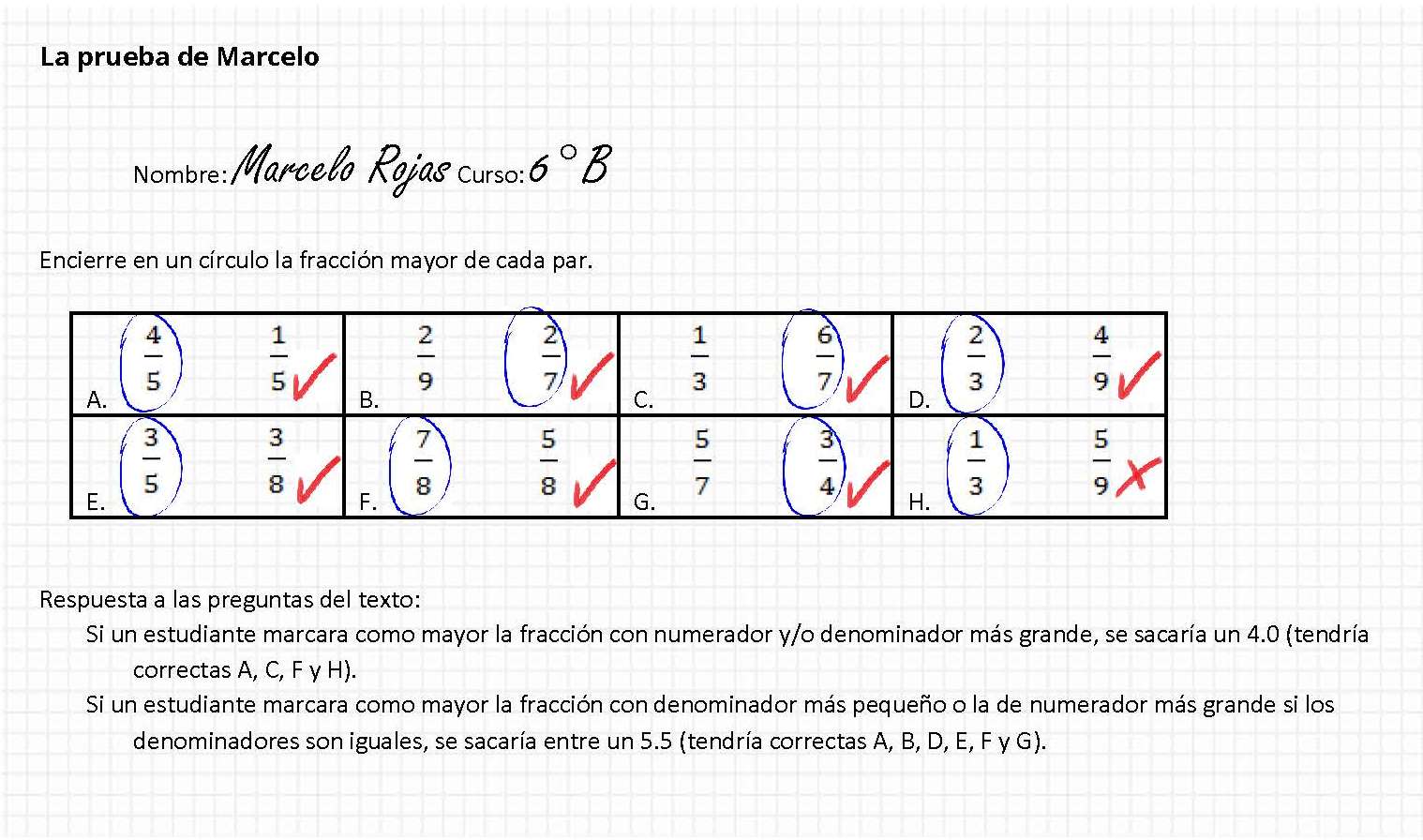
En el recuadro, podemos ver la prueba y respuestas de Marcelo, quien se sacó un 6,3. Esta buena nota, sin embargo, no va de la mano con una comprensión adecuada de las fracciones: el pensamiento de Marcelo considera solamente el número de partes que le falta a una fracción para llegar al todo, sin tomar en cuenta el tamaño de esas partes. Veamos otra pregunta, donde Marcelo se equivocó (ver recuadro): si bien es cierto que a  le faltan dos partes para completar el entero mientras que a
le faltan dos partes para completar el entero mientras que a 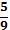 le faltan 4, pero cada parte de las que le faltan a
le faltan 4, pero cada parte de las que le faltan a  es más grande que cada una de las que le faltan a
es más grande que cada una de las que le faltan a 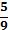 . Lo más importante pedagógicamente es que fijarse sólo en la nota que obtuvo Marcelo no revela cuál es el error que hay detrás, ni da pistas sobre cómo corregirlo.
. Lo más importante pedagógicamente es que fijarse sólo en la nota que obtuvo Marcelo no revela cuál es el error que hay detrás, ni da pistas sobre cómo corregirlo.
Conocimiento pedagógico de la matemática
Cualquiera que haya enseñado matemática a niños en edad escolar coincidirá en que no basta con conocer los contenidos matemáticos a la perfección. Un buen profesor comprende y puede explicar por qué las formas de resolver una ecuación o sumar fracciones "funcionan", y entiende los posibles errores que hay detrás de una respuesta errónea. Es decir, sabe matemáticas y es también capaz de develar el pensamiento matemático de quienes no saben. Esta capacidad es difícil de lograr, sobre todo en casos como el de las fracciones, ya que su enseñanza tradicionalmente se ha enfocado en los métodos para comparación y cálculo, pero sin hacer suficiente énfasis en por qué estos u otros métodos son adecuados o no.
El trabajo realizado en el CIAE, y que contará en el futuro con apoyo de Fondecyt, aplicó una prueba de comparación de fracciones similar a la de Marcelo. Analizando en cuáles ejercicios acertaban y erraban los participantes, se identificó diversos patrones de pensamiento. Por ejemplo, algunos marcaban como mayor aquella fracción que poseía el numerador y denominador más grande; otros marcaban como mayor la fracción que poseía el denominador más pequeño o la de mayor numerador si es que los denominadores eran iguales. ¿Qué nota se sacarían esos estudiantes en la prueba del recuadro? ¿Cuáles preguntas responderían correctamente, y cuáles no?
Los resultados de investigaciones como éstas permiten profundizar nuestro conocimiento pedagógico de las fracciones y reaccionar de manera más adecuada ante estos errores. Por ejemplo, un estudiante que piensa que una fracción es mayor si tiene el mayor numerador y denominador respondería que 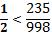 . Él seguramente no ha aprendido que las fracciones poseen una magnitud propia, la cual puede ser pequeña incluso cuando los componentes de la fracción sean enormes, y también tendrá problemas reconociendo que
. Él seguramente no ha aprendido que las fracciones poseen una magnitud propia, la cual puede ser pequeña incluso cuando los componentes de la fracción sean enormes, y también tendrá problemas reconociendo que  . Podría entonces beneficiarse de actividades que enfaticen las magnitudes de las fracciones, como trabajar con la recta numérica.
. Podría entonces beneficiarse de actividades que enfaticen las magnitudes de las fracciones, como trabajar con la recta numérica.
En resumen, reconocer cuál es el razonamiento detrás de una respuesta errada nos permite pensar en estrategias más adecuadas y específicas de intervención. ¿Cómo llevar esto a nuestra práctica?
Fuente: Comunicaciones CIAE